第八章 再谈四维时空
宇宙的终极图景
我们人人都生活在一个四维时空中,其中,空间有三个维度,时间一个维度,我们在四维时空中的运动速度恒定为光速,这是我们在上一章中了解到的内容。把三维的空间拓展到四维,这个并不是爱因斯坦首先想出来的,而是他的大学老师、德国数学家闵可夫斯基首先提出——应该把时间也作为空间的一个维度与另外三个维度整合起来。在他看到学生爱因斯坦的相对论之前,他就有了时间维的初步想法,在看到相对论后,闵可夫斯基恍然大悟,一点就通,数学大师不愧为数学大师,他很快(1908年)就在相对论的基础上建立起了闵可夫斯基时空的数学模型,爱因斯坦对此也是敬佩不已的。下面首先让我们来看看闵可夫斯基的四维时空图是怎么回事,这可是一个相当有趣的模型。
图只能画在二维的平面上,在二维的平面上想表达三维的物体本就已经很困难了,还要学会透视法什么的,现在闵可夫斯基居然想在二维的平面上表达四维空间的运动,那真是具备超凡的勇气和智慧的。闵科夫斯是这么想的:运用二维上的透视法,最多只能画出三个维度的物体形象,这个是我没法改变的,现在我必须要体现出时间这个维度,那么既然如此,我只好牺牲一个空间维度,让我们先把三维的空间压缩成两维的空间,这样我们就能在纸上把空间和时间尽可能地画在一起了。
于是,闵可夫斯基画出了这样一张时空图:
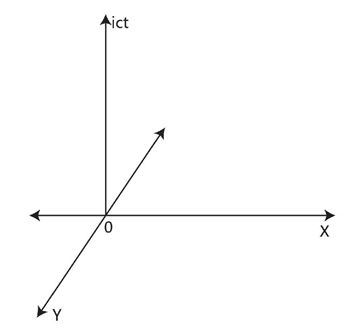
图8-1 闵可夫斯基四维时空基本图
我已经看到了你失望的眼神,你可能满心期待能看到一张惊世骇俗的做梦也没想到过的神图,可惜,看到的就是一张貌似随便找本中学数学课本打开就能看到的图。各位,耐心点,真正精彩的大片往往都是从平淡的开头开始的,鲁迅先生诗曰:“心事浩茫连广宇,于无声处听惊雷。”我觉得形容的正是你接下去将要看到的内容。请先耐着性子听我解释一下,上面这幅图的X轴和Y轴表示空间坐标(把一个空间维度,也就是Z轴给忽略了),并且空间坐标是两端延伸的,表示在空间中可以朝正反两个方向运动。竖着的这根线就是时间坐标(ict),为了让坐标系的单位统一,所以这根坐标的单位是光速c乘以时间t得到的就是跟空间坐标单位一样的距离概念了,那为什么前面还要加一个i呢?在高等数学里面,i表示虚数,也就是说,闵可夫斯基为了表达时间这个维度和空间维度的区别在于时间维只能朝一个方向运动,所以加了一个表示虚数的i以示区别。
闵可夫斯基四维时空坐标的要点是:1.所有的坐标轴互相垂直。2.坐标轴单位统一。3.表示时间维度的轴只能朝一个方向运动。
接下去,我们的思维盛宴要开始慢慢上菜了。第一道菜:如果以地面为时空坐标原点,站在地面上不动的爱因斯坦,他的时空运动轨迹是怎样的?
先思考5秒钟,然后我们上菜:
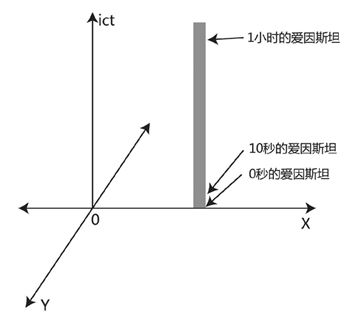
图8-2 爱因斯坦在时空中的轨迹
爱因斯坦在时空中的运动轨迹是一根和时间轴平行的直线,他在空间中没有相对运动,但是在时间中运动,因此时空图如上所画,应该很好理解对吧。闵可夫斯基把物体在时空中运动的轨迹称之为“世界线(World Line)”,这根世界线上的每一个点称之为“世界点(World Point)”,请记住这两个名词,我们后面就直接用这两个名词来说事,可以节省很多笔墨。我想特别提请各位读者注意,世界线是真实存在于我们生活中的宇宙中的,你不能把它仅仅当做是闵可夫斯基的头脑风暴练习,或者是一种假想图,它是一个客观存在,就如同民航管理局绝不能忽视一架飞机在空间中的飞行轨迹一样(如果轨迹计算不精确,可是要撞机的),未来如果有一天成立了时空管理局,那么世界线就会如同现在的飞机飞行轨迹一样重要。
第二道菜:仍然是以地面为时空坐标原点,一列在地面上行驶的高铁,它在时空图中的世界线是怎样的?
可能你脑子里已经有答案了,我们上菜,看看是不是想的一样:
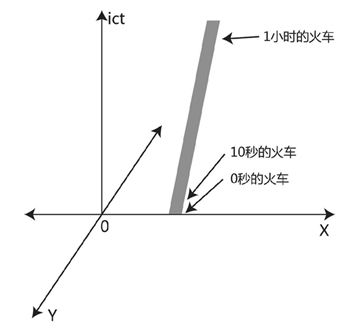
图8-3 高铁运行时的世界线
高铁的世界线是一根斜线,因为它在时间维运动的同时,也在空间维中运动,所以时空轨迹就是一根斜线。
第三道菜:这次如果以太阳作为参照系,请分别画出地球和太阳的世界线。
这次的题目貌似难了一点,地球是绕着太阳做圆周运动的,它的世界线应该是怎样的呢?让我画出来给你看:
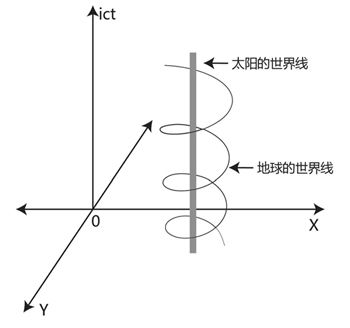
图8-4地球的世界线是一根螺旋线
地球的世界线就像是一条盘绕在太阳世界线上的蛟龙,蜿蜒而上,是一条规则的螺旋线。这次你可能要稍稍想一下才能理解过来,不过我相信这肯定难不倒你,这道菜你还是很轻松地就吃下去了。
第四道菜:以湖面作为参照系,请画出一颗石子扔进湖水中产生的一个涟漪的世界线。
这道菜看上去有点复杂,不知道该从哪里下筷子,别心急,让我来帮你画出涟漪的世界线:
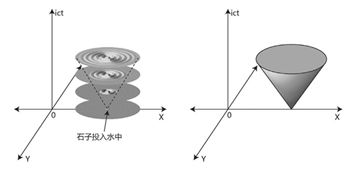
图8-5石子投入湖水,产生的一个涟漪的世界线是一个倒圆锥
湖水中的一个涟漪的世界线不再是一根“线”,因为涟漪无法再被看成是一个“点”了,它的世界线实际上是一个倒放的圆锥体,随着时间的增加,体积不断增大。
第五道菜:以太阳为参考系,请画出太阳光的世界线。
这次可是真正的挑战来了,太阳发出的光不同于一个平面上的涟漪,太阳是一个球体,它向空间的四面八方发出光芒,把太阳想象成一盏灯泡,在点亮的那个瞬间,就会形成一个光球(你可能会想起爱因斯坦的第一个梦“环球快车谋杀案”),这个光球在百万分之一秒就达到了直径600米,一秒后,直径就达到了60万公里,相当于地球直径的47倍,这个光球可以装下10万个地球,这仅仅是一秒钟,真是一个疯狂暴涨的光球啊。
这个光球不同于火车和涟漪,它在空间的三个维度中都在运动,因此我们是不可能准确地在只有三个维度的时空图中画出它来的,但是如果我们忽略其中的一个空间维度的话,我们会发现光球的扩散在二维平面上的投影和湖水的涟漪是一样的,随着时间的增加而不断地向四面八方扩散。于是,如果在忽略了一个空间维度的时空图中画出来的话,太阳光的世界线和涟漪的世界线是一样的。如下图所示:
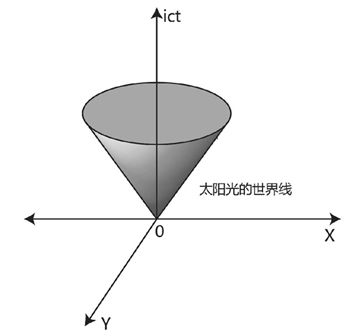
图8-6太阳光的世界线形成了一个圆锥体,称之为光锥
这个由光形成的圆锥体,闵可夫斯基把它称之为“光锥”,当然,真实的四维时空中的光锥是一个四维光锥(或者可以叫超光锥),我们现在看到的只是它的三维近似形状,但是这个四维光锥的基本特点在上面这幅图上是基本准确的,随着时间的增加,光锥的体积迅速地增大。
我们现在是用了一个会发光的太阳作为时空坐标原点,我们很容易就画出了该时空坐标的光锥图。下面重点来了,请一定听仔细,任何一个事件都可以当做是时空坐标原点,不管这个事件会不会发光,我们都可以假想这个事件是发光的,那么就可以画出这个事件的光锥图,这个光锥被闵可夫斯基称之为“事件的将来光锥”。什么叫事件?宇宙中发生的任何事情都可以称之为一个事件,小到一根针落地,大到太阳爆炸,一切一切的事情都可以称之为一个“事件”。
下面,闵可夫斯基为我们隆重献上第一道大菜,这是一个伟大而深刻的发现,它是狭义相对论的一个气势恢弘的推论,直接把我们的视野扩展到了全宇宙。闵可夫斯基在1908年的一次名为《时间与空间》的演讲中向世人大声宣布了他的一个发现:
宇宙中的任何事件都只能影响它的将来光锥内的物体,凡是在事件的将来光锥外的物体不会受该事件的任何影响。
上面这句话有点长,但是请你仔细读一下,这是本章的第一个惊雷,高潮正在慢慢酝酿。可能你没有完全读懂,让我来画一个图示帮你理解:
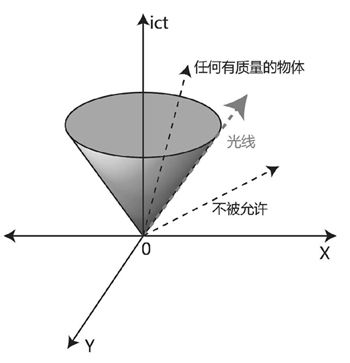
图8-7 任何有质量物体的世界线必在事件光锥之内
根据狭义相对论,任何有质量的物体的运动速度都不可能超过光速,因此事件的光锥是该事件能够影响到的最大时空范围,凡是处于这个光锥之外的东西均不受影响。举个例子,如果此时此刻太阳突然熄灭了,但是我们在太阳熄灭的头一秒钟,仍然处在太阳熄灭事件的光锥之外,那么这个事件不会对我们造成任何影响,我们也根本不可能知道这个事件,只有当8分钟后,事件光锥覆盖到了地球所在的位置时,该事件才对我们产生影响。
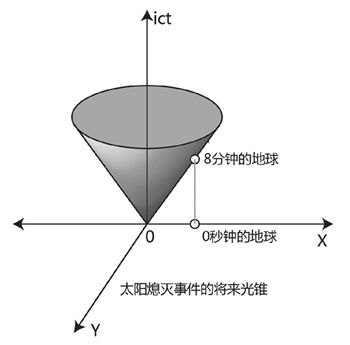
图8-8 太阳熄灭事件的将来光锥8分钟后和地球的世界线接触
千万不要小看这个发现的意义,这是对这个宇宙规律最深刻的发现之一,这个发现告诉我们宇宙是一个“定域”的宇宙,也就是任何一个事件能影响的时空范围是有大小的,不但有大小,而且大小还是固定的一个圆锥形。注意我的用词,我说的是时空范围,并不是空间范围,所以我把时间增大光锥体积增大的情景已经一并说了。
那么请大家继续再往下深想一步,既然现在发生的任何事件对将来的影响是“定域”的,那么过去曾经发生过的事情对现在的影响必然也是“定域”的,既然有了事件的将来光锥,那么同样也应该有事件的过去光锥,过去光锥代表的是过去发生的事件对现在的影响,我们画出图来:
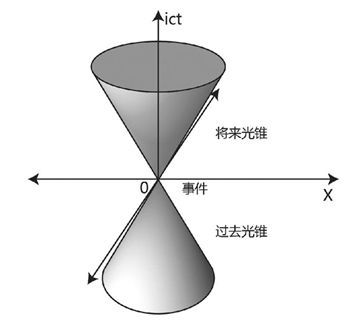
图8-9 事件的过去光锥和将来光锥
事件的过去光锥刚好是把将来光锥倒过来放置,形成一个沙漏的形状,这个不难理解,打个比方就是只有8分钟前的太阳熄灭事件会影响到现在的我,2分钟前的熄灭事件不可能影响到现在的我。
这下你明白国际物理年同时也是纪念相对论诞生一百周年的标志的含义了吗?

图8-10 2005年国际物理年的标志
它就是一个抽象的事件光锥的全貌,喻示着物理学的过去与未来,这个事件光锥与E=mc2一样都是相对论的标志性象征,它蕴涵着深深的宇宙奥秘,足够你我用一生去慢慢回味。
闵可夫斯基的四维时空图和事件光锥的发现深深震撼了爱因斯坦。同时他们两个人心里都明白,这事肯定还没完,宇宙的奥秘只是刚刚露出了冰山一角,四维时空图也只是一幅刚刚展开一点点的卷轴画,这幅卷轴画全部展开后,到底会在人类的面前呈现怎样的一幅全景图呢?闵可夫斯基和爱因斯坦都怀着深深的好奇,他们都迫不及待地想要一览卷轴中的秘密。这一年闵可夫斯基44岁,爱因斯坦29岁,他们一个沿着数学的思路,一个沿着物理的思路继续去发掘时空图中隐藏的秘密。
第二年圣诞节刚过,天气异常的寒冷,闵可夫斯基和两个不满10岁的女儿亲吻道晚安,看着她们甜甜地进入梦乡,然后,他转身回到自己的书房,点亮台灯,迫不及待地开始了演算。最近他为一些新的发现和计算结果感到兴奋不已,他觉得自己已经快要解决狭义相对论的缺憾,那就是狭义相对论不能包含非惯性系的问题。突然,他感到中腹有隐隐的疼痛,闵可夫斯基并没有特别在意,他想可能是吃坏了肚子,没事,挺一挺就过去了;但是很快中腹的疼痛开始向右下腹转移,而且越来越剧烈,很快就疼得他掉下了大颗大颗的汗珠,他一声惨叫,妻子闻声跑过来,看到此情景吓坏了,立即把闵可夫斯基送往医院。但最终抢救无效,闵可夫斯基于三天后去世。科学界的一位重量级人物正值创作力最高峰的时候霍然陨落,实在让人感到万分遗憾。夺去闵可夫斯基生命的其实就是在今天看来毫不起眼的急性阑尾炎,切除它只是现代外科手术中最最简单的一个,任何一个乡镇医院的外科医生都会做,然而它却夺去了闵可夫斯基的生命。若不是闵可夫斯基的意外身亡,第一个完整打开卷轴看到宇宙终极图景的人很可能就不是爱因斯坦而是闵可夫斯基。
闵可夫斯基死后,他生前的挚友希尔伯特(我们第五章结尾提到的希尔伯特空间的发现者)整理了闵可夫斯基的遗作,并且结集出版,而爱因斯坦在看到闵可夫斯基的遗作后深受启发,最终一个人独立完成了广义相对论。广义相对论发现了时空弯曲这个惊人的事实,然后爱因斯坦又从数学的角度推断出宇宙要么膨胀要么收缩,最后由美国人哈勃证实我们的宇宙正在快速膨胀,人类从而认识到宇宙是有一个开始的,很可能开始于一次恢弘的宇宙大爆炸。这些是我们在第五章最后已经了解过的内容,在这里重提此事,因为它事关时空图的终极图景,下面,就让我来为你打开卷轴,让我们一览这个宇宙的终极图像,这是以爱因斯坦为首的广义相对论学家们和天文学家们苦苦追寻了几十年的图像,这是他们日思夜想、梦寐以求的图像:
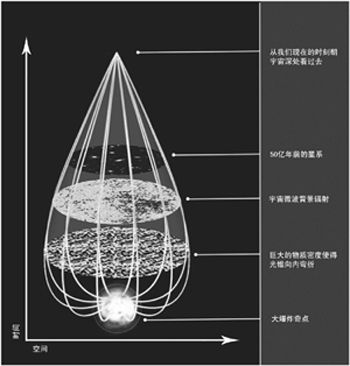
图8-11我们的宇宙图像——果壳中的宇宙
这就是我们这个浩瀚宇宙的终极图像,宇宙的未来还未发生,我们不敢妄言它的图像。但是宇宙的过去我们已经可以看到,请你现在跟我一起闭上眼睛(开个玩笑,闭上眼睛了还怎么看我后面要你想的事情,那就闭上一只眼睛吧),让我们一同想象一下你站在星空下,朝着宇宙的任何一个方向望去,你看到的既是浩茫的空间,也是深远的时间,天上的星星发出的光芒跨越了几万几亿光年达到了地球,你看到的正是几万几亿年前的星星,我们看得越远,就是看得越早,我们每时每刻抬头仰望星空,看到的正是一个过去的宇宙。这个终极的宇宙图景看上去像一个什么东西呢?是不是很像一个坚果呢?比如一颗瓜子,一颗松子,一颗榛子,宇宙的过去光锥就像这个坚果的外壳,包裹着我们的宇宙万物,我们的宇宙是一个果壳中的宇宙。霍金在1988年完成了他的科普巨著《时间简史》后,又在2001年创作了他的第二部科普巨著,起名《果壳中的宇宙》,第三本是新近完成的《大设计》,这三本书的名字起得确实非同凡响,气势磅礴,内容也是层层递进,让人目不暇接。
神奇的四维
本章的内容就像是一首古典交响乐,由平静的序曲开始,逐渐进入主题,然后达到高潮。现在本章的高潮已经来临,让我们一同来继续领略四维时空的奇景。
我们每个人都已经习惯了三维的世界,所有的物体都有长、宽、高的基本属性,我们也很容易知道二维平面的图景,一幅画就是二维的,那么一根线就是一维的,可是我们却怎么也想象不出来四维的物体长什么样,有什么特性。一个三维空间的正方体,我们很容易想象出它们的样子,可是一个四维的正方体,我们称之为超正方体,或者一个超圆锥体、超圆柱体、超金字塔,你能想象出它们的样子吗?这似乎已经在开始挑战我们的想象力极限了,但是不要怕,这不有我在呢,让我帮助你一步步地把四维物体的形象建立起来,我们从研究超正方体开始这段思维之旅。
我们先不用急着直接把超正方体的形象想出来,让我们先来研究一下维度之间的关系,每多一个维度意味着什么?会带来哪些变化呢?
让我们先从一维的世界开始。如果这个世界是一维的话,那么这个世界的生物都是一根线段,只有长度,没有高度和宽度,它们的头尾各有一个眼睛,它们可以在X轴方向左右移动,但是永远也无法超越前面的人,要与隔着的一个“人”打声招呼都是不可能的,更不要说与别的同伴见面,他们只能通过与其相邻的“人”传话过去,一维生物的交流就永远只能是报数,一个挨一个地报过去。
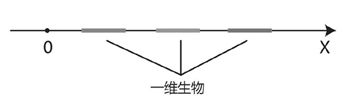
图8-12一维世界中万物都是一根线段
这个一维世界是一个狭窄得让人窒息的世界,在这个世界中自然不可能有任何形状的概念,一切都是线段,那么如果突然有一天,一根一维的线段获得了朝另外一个维度,也就是Y轴方向运动的能力,那么它的运动轨迹会变成什么样呢?让我们画个图来研究一下:
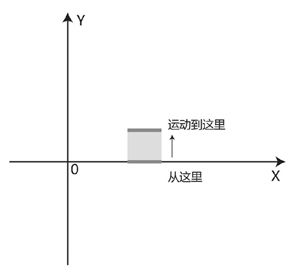
图8-13 一根一维的线段朝Y轴方向运动一段距离后,轨迹形成一个正方形
一维线段只有2个顶点1条边,它在二维方向运动一段距离后,两个顶点就多了一倍,变成了4个,我们把两个顶点运动前后的位置用线连起来,于是我们看到轨迹就形成了一个正方形,这个正方形有4个顶点4条边。一旦从一维的世界拓展到了二维的世界,整个天地豁然开朗,世界从一根只有长度没有高度的“线”突然变成了一幅画,在这个二维世界中,生物可以任意游走和穿行其间,可以跨过相邻的“同伴”直接与别的同伴见面。如果一维生物有感知的话,它们一定会被眼前的奇景所震撼,做梦也想不到居然可以有如此宽广的天地。天地之大令它们难以想象,并且这个二维世界里的物体再也不是只有长度区别的一根线段了,可以拥有如此复杂多变的形状,形状的数量之多简直就是无穷无尽的,一个一维诗人在看到了二维世界的奇观后,带着它奇特的口音由衷地吟出这样的“诗句”:嘛叫宽广,界就叫宽广。
然后,突然有一天,一个二维的正方形获得了在另外一个维度,也就是Z轴运动的能力,那么它的运动轨迹又会变成一个什么?让我们画出图来看一下:
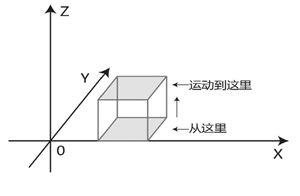
图8-14二维正方形朝第三个维度运动后形成正方体
我们看到,一个二维的正方形在三维方向运动一段距离后,原来的四个顶点翻了一倍,在新的位置又形成了4个顶点,于是我们还是用老方法,把顶点在运动前后的位置连起来,于是形成了8个顶点和12条边(正方形本来有4条边,运动后在新位置又有4条边,然后顶点连线再形成4条边,加起来刚好12条边)的一个正方体。这个世界从二维的画变成了三维的空间,天地开阔了岂止百倍,如果生活在画上的二维生物突然来到了这个三维世界,它再回看自己曾经生活过的二维世界的话,你觉得它会怎么想?它必定会为眼前的景象所惊呆:旧有的世界观一去不复返,原来我们以前那个世界是如此狭窄得令人窒息啊;原来我们认为的牢不可破的监狱根本无法关住犯人,一个犯人如果跟我现在一样能在第三维运动,他只要轻轻一跨,就在看守们做梦也想不到的地方越狱了;原来我们以前那个二维世界的保险箱是如此的不保险,从我现在三维的角度看过去,一切都不再是保密的,保险箱内的东西全都一览无余,轻易就可以取出来。眼前的这个三维世界实在宏大得不可思议,万物不仅仅只有形状,还有体积,无穷无尽的形体变化除了用“难以置信”去形容,实在找不出第二个恰当的词了。
霍金在《果壳中的宇宙》一书中风趣地说二维生物和三维生物的区别在于,二维生物想要消化食物会非常的困难,因为如果他们的嘴到肛门是被一根肠子联通的话,那么他们必然会被一分为二。其实别说肠子了,二维生物的血管会把他们分割成无数的小块,彼此不相连。
下面是重点来了,各位读者务必打起精神。
如果,突然有一天,一个三维的正方体获得了朝第四个维度运动的能力,那么它的运动轨迹会形成什么样的一个形状呢?虽然我们暂时无法在头脑中想象出来,但是根据我们之前的维度增加的经验,我们至少可以推断出,这个四维的超正方体必然有16个顶点(原位置8个顶点,运动后在新位置产生8个顶点),然后有几条边呢?在原位置有12条边,新位置又有12条边,然后把8个新老顶点连接起来又产生8个边,因此,这个超正方体就会有12+12+8=32条边。这样我们就得出结论,超正方体有16个顶点32条边,这样我们就至少可以画出它在三维空间中的近似图,或者认为这是它在三维空间中的投影:
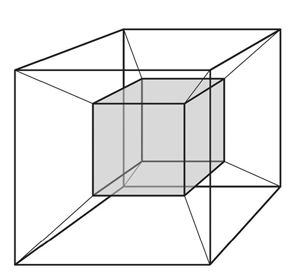
图8-15 超正方体的三维投影
看,这就是超正方体在三维空间的投影,哦,可能有些读者对投影的概念不是很理解,那么我画一个正方体在二维平面的投影图出来,你马上就理解了,这也会帮助你想象超正方体的真正形态:
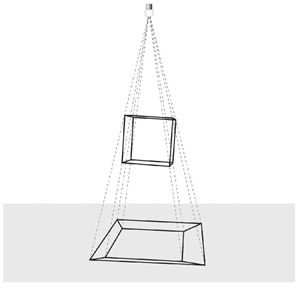
图8-16正方体在二维平面的投影
从上面这幅图中,我们可以看到,物体的投影虽然并不是物体的真正形态,但是它能准确地体现出该物体的基本特征。请把两幅图结合起来,然后,闭上眼睛,努力在脑中冥想一下,过一会儿告诉我你想到的四维超正方体的真正形态是什么样子的。
过了一分钟,你睁开眼睛,然后茫然地告诉我:“大哥,很抱歉,还是没想出来!”
嗯,不奇怪,我料到了,这玩意儿确实不是太容易想,还好我还留着一招后手,让我继续来帮助你做这个思维体操。下面我们来看看,如果你把一个三维正方体在二维平面上展开,会得到一个什么样子的形状呢?换句话说,其实就是把一个纸板箱展开全部平铺在地面上,会是一个什么样子呢?我们画出图来看一下:
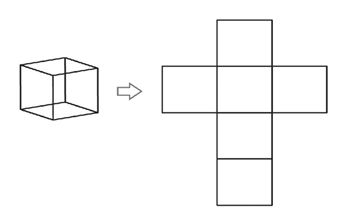
图8-17 正方体在二维平面展开的样子
一个正方体总共有6个面,注意看正方体的二维投影也是6个面,这个基本特征是相当准确的。把6个面展开,就得到了上图所示的样子,其实就是一个纸盒子剪开压平的样子。那么,你能不能画出超正方体在三维空间展开后的样子呢?三维到二维展开的关键是研究总共有多少个“面”,那么从四维到三维的展开关键就是研究总共有多少个“体”,我们从超正方体在三维空间的投影可以数出来,总共是8个“体”,这个基本特征是准确无误的,所以,超正方体在三维空间展开后的样子应该是这样:
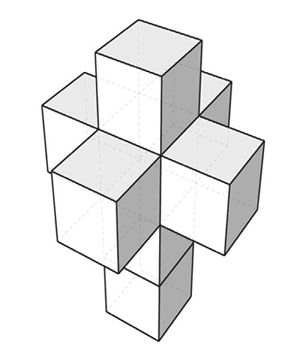
图8-18超正方体在三维空间展开后的形态
于是,我要你再次闭上眼睛,把超正方体在三维空间的投影和展开图都在脑子里面过一遍,然后努力想象一下超正方体的真正形态,你能想象得出来吗?
这次过了整整五分钟,你睁开眼睛,还是一脸茫然地告诉我:“大哥,还是想象不出啊!”
我答道:“别难过,其实,大哥跟你一样,也想象不出来。”
这种状况,就跟作为三维世界中的我们去跟一个二维世界的人讲解什么是正方体一样。在二维世界中,只有正方形,没有正方体,你费尽口舌,举了无数例子,从二维正方形在一维上的投影再讲到二维正方形在一维线段上的展开,然后再画出正方体在二维平面上的投影以及展开图,希望通过类比的方法让二维人想象出正方体的真正形态,口水都讲干了,可是,二维人仍然茫然地看着你,摇摇头说:“大哥,还是想象不出来。”其实,在面对超正方体的想象力上,我们比那个可怜的二维人好不了多少。当一个二维人有一天终于能看到三维的世界后,他的震惊该是多么巨大,他除了不停地重复“难以置信”这个词以外,实在找不出恰当的形容词了。
其实我们人人都生活在四维时空中,理论上说,我们每时每刻都在时间这个第四维上运动,但问题是,时间这个维度是单方向的,因此我们无法回头看见过去的自己,从而也无法感受到四维空间之大。但是,难道就不能有第四个空间维度存在吗?时间可以看成是第五维,四维时空变成了五维时空。如果真有第四个真正可以正反两个方向运动的空间维度,那么我们三维人是真的有可能跨出我们这个世界的“画”,从第四个空间维度俯瞰我们这个世界,请想象一下我们将面对的是怎样一番令人难以置信的奇景呢?
天地之大,你该如何用语言去形容四维空间的宽广呢?我真的是无法形容得出来,但是好在有比我高得多的高手,他就是有中国科幻作家第一人之称的刘慈欣先生,在他的巅峰之作《三体3·死神永生》中对四维空间的奇景有着惟妙惟肖的描述,其逼真感和现场感令人叹为观止,如果你有兴趣想对四维空间有进一步的认识,不妨一读。
如果真有第四个空间维度,那么为什么就不能有第五个、第六个,以至于无穷多个空间维度呢?发出同样诘问的人不仅仅是我,也有全世界许多著名的物理学家,恰恰是这个诘问引领现代物理学家打开了基础理论物理研究的一个全新领域。按照目前最新的理论,我们这个宇宙在诞生的时候总共有10个维度,其中有9个空间维度,1个时间维度,经过百亿年的演化,现在6个空间维度已经蜷缩在了微观世界中。关于这个话题,我们在本书的最后一章还要再次讨论,那又将是一段充满挑战的思维之旅。
好了,关于时空的旅程到此就正式结束了,结束这段时空之旅的同时,我们关于相对论本身是什么的话题也就全部讲完了,我希望这10多万字阅读下来,你终于对相对论有了一个基本的认识,不再觉得相对论很神秘,很难懂了。
但是,相对论结束了,物理学并没有结束,我们的书也还没有结束,因为,好戏还在后头。最后两幕大戏上演之前,我必须先来带你认识一下爱因斯坦的世界观、宇宙观。爱因斯坦对这个宇宙的认识有一个中心两个基本点,先说两个基本点。
第一,爱因斯坦认为这个宇宙是“定域”的,这个概念我们在本章前面刚刚讲到过,也就是说一个事件的将来光锥决定了这个事件对时空的影响范围,而它的过去光锥决定了怎样的时空范围可以影响到这个事件本身,过去光锥和将来光锥都是有大小和形状的,也就是说这个宇宙是一个定域的宇宙,任何事件之间都不可能超越这个范围而产生相互影响;
第二,爱因斯坦认为这个宇宙是客观存在的,宇宙万物的运动规律独立于观察者而存在,不论是否有人的存在,皓月星辰、茫茫星海,它们的运动是一个客观存在。不管是在人类诞生之前,还是人类灭亡之后,宇宙仍然是在按照它自身的发展规律一丝不苟地演化,用宇宙自己的话说就是“我膨胀也好收缩也好,与人类何干。”
围绕着这两个基本点,爱因斯坦还有一个中心思想,那就是“因果律”,宇宙万物有果必有因,有因必有果,宇宙从大爆炸开始的那天起,就在朝着确定无疑的方向演化,不管我们知道也好不知道也好,宇宙的未来早就已经是一本写好的剧本,宇宙必然会按照剧本的要求丝毫不错地演化下去。
爱因斯坦虽然用相对论颠覆了牛顿物理学,但是在因果律这个基本宇宙观上,爱因斯坦和牛顿是一模一样的。牛顿认为,如果我们能够知道某一时刻宇宙中所有物体的运动状态,那么只要拥有足够强大的计算能力,我就可以确定无疑地计算出宇宙的过去和未来,分毫不差。爱因斯坦的名言是“宇宙最让我难以理解之处就在于它居然是可以被理解的”。爱因斯坦经常喜欢拿上帝来说事,还经常称呼上帝为“老头子”,但爱因斯坦实际上是一个彻底的无神论者,他口中的上帝其实指的是斯宾诺莎(西方近代哲学史上最著名的理性主义者,对西方科学思想影响深远)的“上帝”,那就是——宇宙规律本身。
爱因斯坦还有一句名言:“上帝不掷骰子!”这个宇宙万物的演化规律不是靠每次掷骰子出来的随机点数来决定的,“老头子”是一个一丝不苟的人,他过去从没有犯过错误,将来也不会犯错误,宇宙的剧本早已定稿。从这一点上来说,爱因斯坦和牛顿都是属于经典的,他们心中的宇宙是经典的宇宙,是一个温暖、有秩序、一丝不苟的宇宙,或许这也是我们大多数人心目中的宇宙。
然而,我们的宇宙真是爱因斯坦心目中温暖的经典宇宙吗?爱因斯坦心目中的上帝真是他希望的那个一丝不苟的上帝吗?伟大的相对论难道就没有一点破绽吗?自从上个世纪以来,人类在研究微观世界时发现了一系列令人费解的实验结果,从此诞生了理论物理学另外一个重要的分支——量子物理学。爱因斯坦首先是量子物理学的奠基人,然后他自己又对量子物理学发出了一系列的诘难,他自己亲手设计了一个推翻量子物理学基本理论(哥本哈根解释)的思维实验,因为哥本哈根解释让上帝从一个温文尔雅的君子变成了一个疯狂的赌徒。这个著名的思维实验被称之为EPR实验,以爱因斯坦、波多尔斯基和罗森塔尔三个人名字的首字母命名,为什么只能在思维中进行呢?那是因为在当时人类的技术水平还发展不到实验要求的精度。但是在爱因斯坦死后27年,也就是1982年,人类首次突破了技术难关,具备了把EPR实验从思维中搬到实验室的能力了,于是,我们将看到人类首次对爱因斯坦的上帝进行审判,老头子到底是一个和蔼慈祥的绅士还是一个捉摸不定的赌徒,答案即将在下一章揭晓。