第二章 伽利略和牛顿的世界
相对性原理
我们的故事要从400多年前开始讲起（你可能在嘀咕：有没有搞错，相对论不是100年前的爱因斯坦发明的吗，怎么一下子就要多倒回去300年？知足吧，我已经比谢耳朵好多了，他总是从古希腊开始说起），是的，为了让你能充分领略人类在通往相对论这条道路上所经历过的蜿蜒曲折、峰回路转，我们必须回到这条路的起点。
现在请跟我一起回到16世纪末的意大利比萨，此时正值文艺复兴的后期，国富民强，文学、艺术、科学的春风从意大利席卷整个欧洲，空气中弥漫着新世纪即将到来的新鲜气息（中国此时正值明朝万历年间）。在比萨大学的一间大教室里，宫廷数学家奥斯提里欧·利奇（Ostilio Ricci,1540-1603）正在讲台上开讲座，讲台下面坐得满满当当。利奇是闻名全国的著名数学家，一向只在皇宫中为侍童们讲课，他要来比萨大学的消息在几个月前就已经传遍了整所学校。医学系的一个叫伽利略·伽利雷的学生起了个大早，终于抢到了最前排的好座位。
利奇开始讲解数学的新进展——代数学，并且用简洁流畅的手法向大家展示了什么是一元二次方程，并且给出了aX2＋bX＋c＝Y的通用解法的证明，进而开始讲解因式分解的概念以及现场演算了（a＋b）n分解的过程。
利奇熟练的演算和生动的讲解博得了阵阵掌声，他注意到坐在第一排的一个年轻学生自始至终都在聚精会神地听讲，脸上不时闪过兴奋和满足的表情，利奇一下子对这个学生产生了好感，讲课的间隙利奇问道：“同学，你叫什么名字？”
“伽利略。”伽利略回答道。
利奇问：“哪个专业的？”
伽利略说：“我是医学系的。”
利奇说：“啊！真是了不起，学医学的也能对数学如此感兴趣，你一定会成为一名伟大的医生！”
伽利略的脸一下就红了，说：“其实，先生，我不喜欢医学，我更喜欢数学和物理。但是我的父亲希望我能成为一名医生，我为此感到十分的苦恼。”
利奇说：“别泄气，年轻人。你可以自学，大学很短暂而生活很长，追随自己的兴趣，你一定能成功的。不管什么时候，你都可以来找我，我愿意成为你的良师益友。”
伽利略受到了极大的鼓舞，从此更是疯狂地喜欢上了数学和物理，并且经常向利奇请教问题。
我们应该感谢利奇对伽利略的鼓励，虽然使世上少了一名不错的医生，但是却催生了一位伟大的物理学家、天文学家和哲学家。
伽利略在力学和物体运动规律方面的贡献是无与伦比的，是他打下了牛顿经典力学的基桩，而牛顿在这片基桩之上盖起了足以让后人仰视的经典力学大厦。
伽利略第一项最广为人知的成就是提出了自由落体定律，这个定律说的是如果不考虑空气阻力的话，那么任何物体的下落速度都是一样的，且都是呈一个固定的加速度（这个加速度上过中学的人都知道，就是g≈9.8米／秒2）。
伽利略把类似自由落体定律这样的现象和规律统称为“力学规律”。
我们再来看一个伽利略发现的著名的“惯性定律”，其实这就是牛顿第一运动定律（当然，伽利略没有像牛顿那样精确地表述出来，因此这一定律的正式发现权仍然归于牛顿）。伽利略发现这个定律，也是从一个思维实验开始的，这个思维实验具备非凡的智慧。伽利略设想把一个小球放到一个U型管的一端，松手让小球自由滑落，那么这根U型管表面越光滑小球在另一头就能上升得越高，伽利略假想如果能发明一种完全没有阻力的材料，则小球应该能恰好在另一头到达跟起点同样的高度。这个现象就好像在一根绳子上挂一个小球做一个钟摆，如果完全没有空气阻力的话，小球从一头摆到另一头的高度应该是完全相同的。
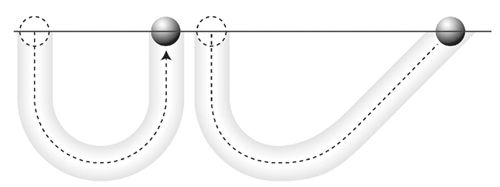
图2-1：小球从U型管一头落下应当滚到相同高度，钟摆每次都应当摆到相同高度
伽利略的这个思维实验没有停，他继续往下想：好，现在假设找到了一种完美的材料，那么我把U型管的另一端拉平，则小球从起点滑落后，为了能在终点达到和起点同样的高度，它只能不停地，永远地滚下去，不可能停下来。
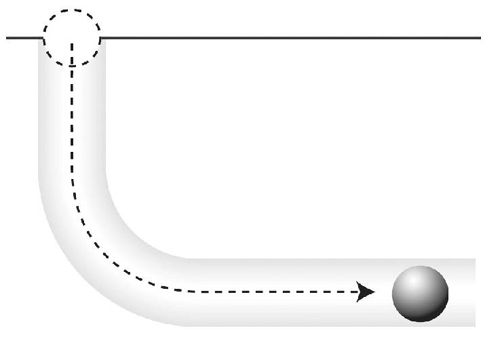
图2-2：如果U型管的另一端是平的，小球就永远不会停下来
从这个思维实验中，伽利略得出了他关于运动的又一个力学定律，那就是在一个完美光滑的表面运动的物体，会有一种保持这个运动的“惯性”，除非有外力阻止这个惯性，伽利略称之为“惯性定律”。
自由落体定律和惯性定律我相信对于各位读者来说都是再熟悉不过的物理常识了，但是在400多年前能有这样的认识那可是大大的了不起，你或许想我要是能回到过去就好了，轻易就可以成为一名伟大的物理学家，这好像也不难想到嘛（本书的后面还真要讲讲时间旅行方面的内容呢）。讲到这里，我就要抛出本章的重点了，那就,是伽利略相对性原理。因为你通过上面的阅读已经知道了什么是力学规律，有了这个基础，我们就可以继续往下了。
伽利略相对性原理：在任何惯性系中，力学规律保持不变。
“得，我好不容易理解了什么是力学规律，你又马上冒出个‘惯性系’这个专业术语，你丫就是喜欢得瑟，能不能别卖关子，说点人话好吗？”边上一位同学看我打下上面的字后，忍不住就开始鄙视我。
莫急，我这就开始解释“惯性系”是什么意思。
为此，我们来假想一个伽利略和你之间的穿越时空的对话。
伽利略：“我想问你一个问题，怎么区分静止和运动？”
你：“这也叫问题？我开着法拉利一溜烟儿地从你身边开过，我就是在运动，难道这有什么不对？”
伽利略：“对不起，请问法拉利是谁？”
你：“哈，不好意思，忘记你是古人了，那我就不说法拉利了，我们说火车吧。”
伽利略：“火车？”
你崩溃状：“你那个时代连火车也木有！！伤不起啊！想想也是，蒸汽机还没发明，瓦特都没出生，好吧，那我们说船总可以了吧，船你总知道吧？”
伽利略：“船，当然知道，你的意思是说如果你在开动的船上，我在岸上，那么我就是静止的，你就是运动的对吗？”
你：“哈哈，我可不会上你的当，好歹我也学过几年物理，我知道你要说的是什么，我替你说了吧。说到运动，必须要有一个参照物，如果以你为参照物，那么你是静止的，我就是运动的。如果反过来以我为参照物，你就是运动的。对不对？你还真以为我是文盲啊，伽利略先生。”
伽利略：“未来人果然牛啊。那好吧，我们继续，现在假设你在一个没有窗户的船舱里面，完全看不到外面的情况，你有没有办法知道船是相对于我运动的还是静止的？”
你想了想：“你这个问题也难不倒我，如果船不是以匀速直线运动在开动的话，我很容易知道船是不是在开。如果船是加速的，我会感到有一股无形的力在把我向后推，如果船是减速的，我就会不由自主地往前踉跄。我天天坐地铁，对这种感觉太熟悉了。呃，你就不用问什么是地铁了，跟你解释不清，反正以此我就可以判断船是在加速还是在减速了。我说得没错吧？伽利略先生。”
伽利略：“完全正确。那如果船的加速度很小，你又是固定在座位上的，很难察觉到微小的推背感的时候，你该用什么办法来判断呢？”
你：“这个……让我想一下。有了，这也不难，我只要做一点力学实验就可以了，比如我用绳子挂一个小球，看这个小球是不是完全垂直的；或者，我把一个小球放在一张平稳的桌子上，我看小球会不会自动滚起来。通过很多的力学实验我都可以发现船的运动状态。”
伽利略：“回答得完全正确，确实不能小瞧你。这也就是说，如果船做的不是匀速直线运动的话，在船上的力学实验的结果会被改变，换句话说，力学规律会被改变。比如惯性定律、自由落体定律（自由落体的方向和加速度都有可能改变）等等。但是，如果现在假设船是在做着完美的匀速直线运动的话，你还能通过力学实验来知道船是否在运动吗？”
你：“那显然就不可能了，如果船舱里面没有窗户的话，我就根本不可能判断出我是静止的还是运动的，不论我做什么样的力学实验，我都无法知道。”
伽利略：“是的，也就是说，在匀速直线运动状态下面，所有的力学规律和你在静止的状态时都是完全一模一样的。况且，你也知道，没有什么所谓真正的静止，我们地球也是运动的，在地球上的每一个人哪怕站着不动，也在随着地球一起运动，运动不运动的关键在于怎么选取参照物。”
你：“我感觉，被你这么一说，静止和匀速直线运动这两个词好像失去了准确的意义，我根本无法定义自己到底是静止的还是在做着匀速直线运动，静止和运动永远都是相对的。”
伽利略：“你越来越接近真理了，没错，用我的话来说，静止和匀速直线运动这两个词的物理意义是相同的，或者说都是不精确的，我用了一个新的词来统一他们所描述的状态，这个词就是‘惯性系’。比如你站在岸上和你在一艘匀速直线运动的船舱里面做实验，在我眼里，你都是在一个惯性系里面做力学实验。我的相对性原理说的就是：在任何惯性系中，力学规律保持不变。”
你：“哦，原来说来说去就是这个啊，嗯，不难理解，我完全同意。”
伽利略的相对性原理对于我们现代人来说，是相当好理解的，但是请大家千万记住这个原理。在后面我们还会提到这个原理，它跟相对论的诞生可是有着莫大的关系，但是你千万别把伽利略的相对性原理当做是相对论了。
伽利略变换式
伽利略在提出了相对性原理之后，觉得用一句话来表述这个原理还是显得不够简洁、不够酷。伽利略想，好歹我也是个数学家，我怎么着也应该用数学的语言来描述我发现的这条伟大的原理吧。于是没过多久，伽利略就提出了几个数学公式，用来描述相对性原理。后人把这几条数学公式就叫做伽利略变换式。在我们现代人眼里看来，这个变换式其实是相当简单的，只需要用到一点点小学数学知识即可，现在我要给大家出一道小学数学的应用题（别怕别怕，我知道你已经N年没有解过数学题了，但我保证这道数学题能勾起你很多美好的童年回忆）：
小明和小红一起来到公交车站，两人见面以后互相对了手表确定了时间，小红要坐的车先来，小红登上公交车开动的时候刚好是7点整，公交车以10米／秒的速度开走了。问：1分钟以后小红距离小明多远？小红和小明的手表分别是几点？
麻烦你别跳过上段，稍稍有点儿耐心，看一下我们的问题。可能你脑袋里面一大堆问号，怀疑是不是我又在出脑筋急转弯的题了。小明和小红的手表走时完全准吗？公交车走的是直线吗？小明在一分钟内确实没动吗？你这个距离是按照公交车头还是车尾算？小明是一直站着的吗？真的没趴下来？
我理解你这种心情，社会上混久了，总觉得简单的背后藏着什么陷阱。我现在很诚恳地告诉你，确实没有任何陷阱，忽略你的那些疑惑，这就是一道小学数学应用题。下面是解法：
1．一分钟等于60秒。小红距离小明的距离S＝vt＝10×60＝600（米）。
2．小明和小红的手表都是7点01分。
上小学的时候，为了解这道题，老师一般喜欢给我们画一幅下面这样的图来解释这道题目：
图2-3：这道数学题图示
看到这幅图，有没有勾起点儿童年的记忆。好了，从这道题目出发，我们继续往下深入一步，我把这道小学数学题改写为一道初中数学题，如下：
小明和小红各自代表一个坐标系的坐标原点，且初始位置相同，有一只大懒猫在小明的坐标系中的坐标x处睡大觉，此时小红以速度V沿着X轴方向做匀速直线运动，t时间以后，设大懒猫在小红的坐标系中的坐标为x’（注意这个是x一撇），求x’和x之间的关系式以及小明的时间t和小红的时间t’之间的关系式。
我知道你对上面的题干看了不止一遍，读上去有点拗口，看上去也有那么一点儿专业了，但其实这道题目实质上和上面那道小学题是完全一样的，所要运用到的数学知识跟第一道题目完全一样，我们看一下这道题目的图解：
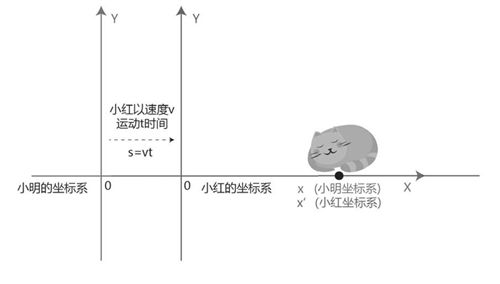
图2-4：数学题图示
画完上面这个图解，我必须顺便提一下，像这样一根横着的X轴加一根竖着的Y轴的坐标系叫做直角坐标系，这是数学家笛卡尔发明的，我们在高中的时候还学到过一种极坐标系，那个只需要一个极点和一根极轴就够了（任何一个点的坐标是用到极点的距离和与极轴的夹角来表示），但是直角坐标系因为特别容易理解，所以用得最广泛，以至于我们经常省直角两个字，直接叫坐标系。我教你一个“装”的招数，就是下次遇到机会就这样说：“各位，首先让我们来构建一个笛卡尔坐标系……”加上笛卡尔三个字，听众立马就会觉得你很厉害。如果你只是平淡无奇地说：“各位，首先让我们画个坐标系。”这效果立马大打折扣。
言归正传，就着上面的图解，我直接写下答案，我想你一定能理解的：
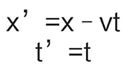
以上这两个数学表达式我们称之为伽利略变换式，我知道你此时正在想：x’到x的变换马马虎虎还能算个数学公式，不过也真是够简单的，但这个t’＝t真是要让我喷饭了，这算啥意思？就是告诉我们小明的手表过去了几分钟，小红的手表也过去了几分钟吗？这也需要伽利略来当做一个伟大的定理告诉我们？不可思议啊不可思议，我要是能回到古代多好啊，我也能成为像伽利略一样牛的科学家。
你先不用这么愤愤不平，让我来解释一下这两个数学表达式的伟大意义。坐标X我们可以把它抽象地认为是小明眼中的世界，而坐标X’我们可以抽象地认为是小红眼中的世界，那么有了这个关系式以后，只要知道了小红的速度和时间，我们就能把小红眼中的世界转换为小明眼中的世界。嗯，上面几句话我承认还是有点费解，所以我需要来举例子了。
现在你想象一下小红在一艘匀速直线开动的船舱里面做各种各样的力学实验，测量各种实验数据来推导各种力学定理。力学实验要测量什么？你仔细一想，你会发现，所有的力学实验对于物理学家来说只需要测量两样东西，一个是坐标（比如小球的起点坐标和终点坐标），一个是用一个尽可能精确的钟表测量时间（当然通常还要测量一个质量，不过那个一般都是一次性测量或者取一个标准质量的物体）。所有的力学实验无非就是测量各种各样的坐标和时间的数据，然后从这些杂乱的数据中寻找普遍规律，从而总结出力学定理。
现在小红是一个在船舱中做实验的物理学家，小明是一个站在岸上的物理学家，对于同一个实验，小红以自己为参照系可以很方便地测量出来一堆的数据，但是你想想如果小明也想测量小红所做的那些力学实验的数据，他该怎么办？小明既没有千里眼，也没有千里手，船每时每刻都在离他而去，小明对此只能望洋兴叹。
伽利略突然出现了，他看着愁眉苦脸的小明。
伽利略微笑着说：“不用发愁，山人自有妙计。”
小明问：“什么妙计？”
伽利略说：“你只需要知道船的速度即可，剩下的事情就都好办。”
小明说：“船的速度不难知道，测出来以后接下来怎么办呢？”
伽利略说：“你只要让小红把她测量到的所有实验数据下船以后给你，然后我给你我这个强大的伽利略变换式，你就能把她测得的所有坐标数据和时间数据变换成以你为参考系的数据。”
小明说：“原来如此，伽利略你真了不起！”
于是，小明按照伽利略的办法如愿得到了所有他想要的实验数据。然后，小明和小红分别用自己手头的数据开始研究力学定律了，研究完毕，两人把他们各自总结出来的规律一比较，竟然完全一致。
你看，有了伽利略变换式，我们就能证明对于同一个力学实验，不管是站在小明的角度观测，还是站在小红的角度观测，所得到的规律是相同的。这说的不就是伽利略相对性原理吗？看来伽利略还真是有点不简单。
大家是否还记得我们在上中学的时候学过一个关于自由落体的定理：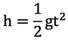
，这个定理告诉我们的是，只要知道物体下落的时间，我们就能算出物体下落的高度。
我本来想以这个为例子来说明虽然通过伽利略变换后实验数据的绝对值变了，但是最后用数学的方法倒腾来倒腾去，等式两边同时加加减减，居然所有的差异都神奇地抵消了，最后总结出来的公式不论是在小明的参考系中还是在小红的参考系中都是完全等价的。但是考虑到很多人对数学公式的天生惧怕，我别弄巧不成反成拙，偷鸡不成蚀把米，反而吓跑了各位耐心的读者，那就悲剧了！因此，我还是不卖弄数学风骚了。
伽利略变换式的伟大意义就在于他用数学的方法证明了伽利略相对性原理。
说到这里，我相信各位读者已经完全理解了伽利略相对性原理和伽利略变换，一点儿都不难理解。正因为简单好懂，符合我们日常生活中观察到的所有现象给我们造成的印象，因此，伽利略大侠的这一原理、一变换就像是倚天剑、屠龙刀，统治了物理学江湖长达200多年之久。在200余年的时间里，无人不臣服，无人敢于挑战，就好像此刻的你不也认为这是天经地义的事情吗？难道这真有可以挑战的地方吗？是的，200多年后一个叫洛伦兹（Lorentz,1853-1928）的侠士拿着一把锈迹斑斑的大刀，向伽利略变换发起了挑战，并且竟然一刀就将伽利略变换这把屠龙刀斩为两截。随后，一个26岁的年轻人，无门无派，不知道从何方冒出来，也携一把木剑向伽利略相对性原理这把倚天剑发出了挑战，这一战那真叫是刀光剑影，霹雳惊雷。这个年轻人，姓爱因斯坦，名阿尔伯特，那真是一位500年一遇的奇男子。当然，这些是后话，且听我慢慢道来。
1642年1月8日凌晨4点，在其故乡意大利，78岁的伽利略走到了人生的尽头，他不断地重复着一句话：“追求科学需要特殊的勇气。”声音越来越轻。终于，伽利略吐出了最后一口气，合上了眼睛，一位科学巨星陨落了。冬去春来，斗转星移，整整一年后，在英格兰的林肯郡有一名男婴呱呱坠地，一位新的科学巨星诞生了，力学的接力棒从伽利略手上交到了这名男婴的手上，这名男婴叫做艾萨克·牛顿。
史上最牛炼金术士牛顿
牛顿是历史上最伟大的炼金术士（没有之一），是最伟大的物理学家、天文学家、数学家、自然哲学家、神学家之一。纵观古今中外所有的“家”们，能集如此众多的“家”于一身的，古往今来就只有牛顿一人。不但空前，而且必将绝后，因为现代科学的分支越来越细，研究越来越深，任何一个领域想要成为“家”都得穷其一生才行……打住打住，你说什么？牛顿是最伟大的炼金术士，还没有之一，真的假的？对于这个事情，我没有半分开玩笑的意思，是千真万确的。牛顿用其一生追求点石成金之术，不过没有证据说明他是为了财富才炼金，我想他去炼金也应该是出于对大自然奥秘的追求。牛顿自己多次说过他最大的兴趣是炼金术，而且他用自己的实际行动证明了这一点，他流传下来的关于炼金方面的著述超过五十万字，他在炼金方面花费的时间相当于他在其他学科所花费的时间的总合。但大多数人都不知道牛顿是炼金术士，主要还是因为他在这个方面没有成就，因为以当时人类对自然科学的认识，是不可能掌握点石成金之术的。
说到牛顿在自然科学方面到底有哪些贡献，那真是可以用多如牛毛来形容。在物理学方面，他提出了著名的牛顿运动三定律，以及质量守恒、能量守恒、动量守恒等定律；在天文学方面，他发现了万有引力定律（还记得那个苹果掉在牛顿头上的传说吗？苹果只是个传说，别太当真），发明了反射式望远镜；在数学方面创立了微积分；在光学方面发现了色散现象，牛顿环现象，写出了《光论》；在经济学方面，奠定了英国的“金本位”体制（牛顿是英国皇家造币局局长）。这个清单如果继续往下还能写得很长很长，但是上面说的这些你都可以在看完本书后忘掉，只有一样，你一定要记住，记住这一样，以后跟人谈起牛顿，你只要一提起，人家就会认为你对牛顿了解得不少，那就是你一定要记住牛顿写过的一本书。李敖曾说过“牛顿其人，500年不朽；牛顿其文，1000年不朽”，就是指的这本书（虽然有大量的证据表明李敖是一个科盲，也没读过牛顿的这本书，但是这句话说得还算靠谱）。书名全称叫做《自然哲学的数学原理》（Philosophiae Naturalis Principia Mathematica），我们一般简称为《原理》。这本书代表了经典物理学的巅峰，牛顿把从大到天上的皓月星辰，小到地上的潮起潮落，一切的自然规律都纳入到了他那本震古烁今的《原理》中。这本书就像是神话中的魔法书，读懂了它就可以预测一切天文奇观。我们前面说过伽利略为经典力学打下了基桩，牛顿在上面构筑了雄伟的大厦，而《原理》就是这座大厦的丰碑，希望你能记住。好了，毕竟我们这本书是讲相对论的，不是给牛顿著书立说，总之我们只要知道一点，牛顿是一个光芒万丈的天才科学家即可。对了，他的墓志铭必须要说一下，诗人波普为牛顿所作的墓志铭中写下了这样的名句：
自然和自然的规律隐藏在黑夜里，上帝说：降生牛顿！于是世界就充满光明。
看看，诗人就是诗人，你说牛顿哪里还是个人，简直就是神的化身啊。你说就这么一个神一样的人物，用了自己生命的一半时间去研究炼金术，这世界上还有谁能比他炼得更出色？牛顿炼金炼累了，顺便想一下物理、数学、天文的事情，想出来的东西就够我们后人仰视一辈子了，这样的人如果还不是史上最牛炼金术士，谁敢是？
但我们毕竟要说的是相对论，因此，说牛顿，我只谈他跟相对论有关的内容，牛顿在其他方面的成就我就不再多说了。
牛顿的绝对运动观
下面，我要虚构一段牛顿在剑桥大学给物理系的新生们授课的场景。有史料表明牛顿的讲课水平出奇的烂，据说常常在他的课堂上，到第一节结束的时候，座位上的学生已经寥寥无几，牛顿只好对着空荡荡的教室快点把剩下的内容讲完，然后匆匆回到实验室做研究去。以至于后来牛顿把每节课的时间减少到15分钟，这样才不至于要对着空气讲课，可见，牛顿实在不能算得上一个称职的老师。但为了让各位可敬可爱的读者能坚持看下去，我会尽可能地把牛顿的这个短板补上，把这个课讲得有趣一点。特别申明，场景和对话纯属虚构。
牛顿说：“同学们，上课了！下面开始点名。Tom,ok,Jerry,ok，嗯，不错，今天来了两个，比昨天多了一个。今天我们要讲的是时间、空间和运动。
“我们假设有一艘船正以10米／秒的速度开着（画外音：船，怎么又是船，我说你就不能新鲜点吗？换个火车啥的。唉，我也不想啊，那个时代没有火车、飞机、火箭，能开的东西不是马车就是船，所以那会儿的物理学家一说起运动，就只能说船，但我跟你保证我们这本书的后面不但有飞机还有宇宙飞船，包你过瘾），Tom，现在我把你扔在船尾，你以1米／秒的速度朝船头方向走动。Jerry，你站在岸上，我想问一下，Tom在你眼里的速度是多少？Jerry，Jerry，这才刚开始你怎么就打瞌睡了，振作点，这还有读者呢！好吧，Jerry，看在你这么诚恳地看着我的分上，我就不难为你了。
“我们利用伽利略变换式可以很容易的就算出，在Jerry的坐标系里面，Tom的移动速度是船的移动速度加上Tom自己走路的速度，也就是10＋1＝11米／秒。
“那么，问题一：如果Jerry自己在岸上用2米／秒的速度和船做同方向运动，在Jerry眼里Tom的速度是多少呢？问题二：如果Jerry和船做着反方向运动，在Jerry眼里Tom的速度又是多少呢？
“我们再次利用伽利略变换，可以算出，问题一是10＋1－2＝9米／秒，问题二是10＋1＋2＝13米／秒。Tom ＆ amp; Jerry，你们的老师我如此婆婆妈妈啰啰唆唆地问你们这些看似很无聊的问题，是希望你们能自己总结出速度合成的规律，给出速度合成的定理。怎样，你们俩个谁先表现一下？”
Tom举手，说：
“教授，我知道了，假设A的速度是V,B的速度是U，那么他们的相对速度W的公式是：
W＝v±U
“取加号还是减号关键看两个速度的方向，如果一致就取减号，否则取加号。”
牛顿说：“非常好。那么，Jerry，你同意Tom的结论吗？”
Jerry说：“我完全同意，教授。我想补充说明的是，速度到底是多少，绝对不能脱离参考系，同样运动的物体，在不同的参考系中，速度是完全不一样的。比如，在我眼里Tom的速度是11米／秒，但是如果从一个站在太阳上的人眼里看来，Tom的速度还得再加上地球绕太阳运行的速度。”
Tom说：“我再补充一句，当我们说某某的运动速度是V的时候，必须先设定该速度的参考系，否则就会失去物理意义。按照这个道理，速度也不存在绝对的快慢。当我站在船上Jerry站在岸上，在船上飞舞的苍蝇眼里，Jerry运动得比我快；反过来，在岸上飞舞的苍蝇眼里，我运动得就比Jerry快。”
牛顿说：“说得很好，你们两个今天果然精神多了，有观众和没有观众真是不一样啊。但是接下来我就要问你们一个有深度的问题了，请问，什么东西可以做参考系？”
Tom ＆ amp; Jerry异口同声地说：“任何东西都可以做参考系。”
牛顿说：“很好，那空间本身是不是也可以做参考系？”
Tom ＆ amp; Jerry：“呃……这个，还真是没想过这么深奥的问题。”
牛顿说：“请你们想象一下，宇宙中充满了空间，宇宙延伸到哪里，空间就延伸到哪里。这个巨大的空间本身代表的就是宇宙的母体，处处均匀，永不移动，所有的东西，天上的星星，地上的蝼蚁，我们所居住的地球都在这个空间中运动。如果把空间本身看做是一个参考系，这个参考系就是一个‘绝对空间’，所有物体在这个参考系中的运动速度就是一种‘绝对速度’，他们就可以比较快慢了，我们会发现，原来地球的绝对运行速度比太阳的绝对速度要快。”
Tom说：“教授，您的这个思想真是太深刻了，学生佩服。”
Jerry说：“可是，我还是有点无法理解。”
牛顿说：“Jerry，在上帝的眼里，我们的宇宙就像一个巨大的玻璃球，玻璃球中充满了水，水安安静静地待在那里，没有一丝一毫的流动。太阳星辰和我们就像水中的鱼儿一样在里面游动，鱼儿感受不到水的存在，我们也同样无法感受到空间中的某样实体的存在。亲爱的Jerry，就像水充满宇宙这个大玻璃球一样，我们的宇宙也被一种叫做以太的物质充满，宇宙万物的运动都相对于这个以太有一个绝对速度。你能理解了吗？亲爱的Jerry。”
Jerry说：“是的，教授，我理解了。但是，您说的这个以太总是让我心里有点不安，因为他无法被我们所感受到，根据我们老家奥卡姆很流行的一句话来说，似乎这样的东西就跟没有是一样的。教授，您能设计一个实验来证明绝对空间的存在吗？”
Tom说：“我说Jerry，你是不是想多了，教授是多么伟大的人，他的思想还能有错吗？”
牛顿说：“不，Tom，别这么说，我可不是胡克（牛顿当时很讨厌的一个物理界的权威，他发现了胡克定律，也就是弹性定律，我们中学都学过）那个小矮子，不容得别人质疑。我是站在巨人肩膀上的人，当然比胡克那个小矮子看得远点，哈哈哈！Jerry，你提的问题很好，我已经想到了一个思维实验来证明绝对空间的存在。”
牛顿水桶实验中的绝对时空观
牛顿转身在黑板上画了一个大大的水桶的俯视图，又在水桶的里面画了一些水，要不是牛顿一边画一边解释这是什么，Tom ＆ amp; Jerry都会以为牛顿在画大饼。
牛顿说：“我们下面来做一个水桶实验。Jerry你看到我画的这个装着半桶水的水桶了吗？外面这一圈就是桶壁，里面都是水。
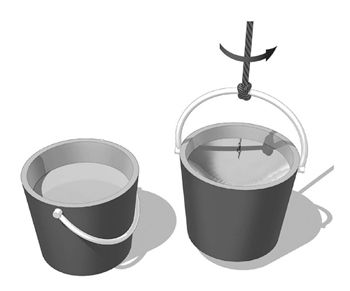
图2-5：牛顿的水桶实验
“现在Jerry你想象你的身体突然缩小了，缩得很小，然后我把你固定在水面附近的桶壁上，让你可以很方便地看到水的状态。注意了，我现在用一根绳子把水桶给吊起来，然后我把水桶这么用力一转，于是水桶就转起来了。Jerry，你在水桶里面感觉好吗？”
Jerry说：“教授，感觉很不好，我的头要晕了，我的眼睛在冒金星。”
牛顿说：“坚持住，孩子，集中精神，观察水面。”
Jerry说：“放心吧，教授，我能坚持。”
牛顿说：“Tom，我已经跟你们讲过我的第一运动定理，物体会保持自己的惯性。所以，水桶在刚刚开始旋转起来的时候，整个水体因为要保持惯性，所以不会马上跟着转起来，水桶会转得比水快很多，这一点不用怀疑。那么在水桶刚开始旋转起来的时候，在Jerry眼里看来，水相对于他开始转动起来了，我们现在向Jerry求证一下，看看是不是这样。Jerry，快点告诉我你看到了什么？”
Jerry说：“教授，我听到你跟Tom说的话了，正如你所说，我看到水转动起来了。”
牛顿说：“很好，Jerry，我们都知道一个旋转的物体会产生向外的离心力（准确地说是向心力），这个离心力表现到一个呈圆柱形的水体中，就会使得水面中心向下凹陷，这是我们在生活中经常观察到的现象。Jerry，你看下水面发生了什么？”
Jerry说：“教授，我看到水面依然平静如故，没有往下凹陷，这可真奇怪了，我明明看到水在围着我转动啊？”
牛顿说：“Tom，看到了吧，在我们眼里，转动刚开始的时候水面不凹陷非常正常，因为在我们眼里水由于惯性还没转起来嘛。换句话说，水相对于绝对空间尚处于静止状态。现在我们稍等一下，因为水的黏着力，我们会看到最终水桶会带动着水一起开始旋转了，最后，水相对于桶壁上的Jerry来说，静止了。Jerry，你现在看到了什么？”
Jerry说：“教授，我看到水越转越慢，越转越慢，现在已经不动了。哦天哪，太不可思议了，水面凹下去了，这真是我这辈子见过的最不可思议的景象，水面凭空就凹下去了，但是又没有旋涡，就好像水面上面有一个无形的大铁球把水给压下去了一样！”
牛顿说：“你看，在Jerry眼中的神奇景象，在我们眼里看来平常无奇，原因很简单，此时的水相对于绝对空间开始旋转起来了，这个旋转的本质不因观察者所取的参考系而改变。好了Jerry，我现在把你复原，你回来吧。”
Jerry擦着汗说：“这真是一次奇妙的经历，教授！”
牛顿说：“让我们再来回顾一下刚才那个水桶实验，如果运动都是相对的，没有一个绝对参考系的存在的话，那么Jerry应该看到水面是先凹后平，但是实际上Jerry和我们一样都看到了水面是先平后凹的，这就是绝对空间存在的证明。”
牛顿得意地说完，看着Tom和Jerry，俩人还愣着呢，一时半会儿反应不过来。牛顿的水桶实验虽然具备大智慧，但却并不能让所有人满意，物理学界对这个实验的质疑声从来就没有停过，但毕竟牛顿的光芒实在太耀眼了，其他人的声音很难发得出声响。
Tom说：“教授，你的这个思维实验太伟大了，我折服了。”
Jerry说：“教授，我恐怕一下子还不能完全理解，让我回去再想想。”
牛顿说：“Jerry，看不见摸不着而又真实存在的东西有很多，不止是以太，还有一样东西，你也看不见摸不着，但是我们谁也无法否认它的存在，那就是——时间。你们说说看时间是什么？”
Tom说：“时间就是生命，时间就是金钱，时间就是知识，时间就是胜利，时间就是丰收，时间就是灵感，时间就是思考。”
Jerry说：“时间就是教堂的钟声，时间就是太阳的东升西落，是斗转星移，我说不清楚时间是什么，但我分明感受到时间在流逝。”
牛顿说：“时间是它自个儿的事情，它真实存在但又与外在的一切事物都无关，它绝对地、均匀地流逝，不与任何性质相关，任何力量都无法改变它绝对不变的频率。威斯敏斯特大教堂的钟声12点整敲响，它就是12点整敲响，不会因为你在洗澡还是在跑步而改变它12点整敲响这个本质。Tom在伦敦，Jerry在巴黎，如果忽略声音的传播时间的话，当钟声响起的时候，你们都应当听到钟声，在听到的那一刹那你们俩若有心灵感应，你们会同时感受到对方传递的感受。时间对于世间万物都是公平的，上帝他老人家既像一个慷慨的施主又像是一个超级吝啬鬼，不论你是国王还是乞丐，他老人家从不……”
此时，下课铃响了，Tom ＆ amp; Jerry几乎是在和下课铃声响起的同时消失在教室门口了，消失速度之快甚至让牛顿都怀疑时间是不是真的存在。
“……多给一点也不少给一点。”牛顿对着空气（他早就习惯了）把最后一句话说完，也夹着讲义走出了教室。
牛顿的时空观符合我们大多数人的日常生活体验，因此，对于牛顿的这套思想体系我相信也很容易被各位读者所接受。况且，和牛顿的想法一样本身就是一件多么值得自豪的事情啊，牛顿是如同神一般的存在，他是当时物理界的泰山北斗，他是物理界的教皇，牛顿说出来的话就像是来自上帝的启示。牛顿的绝对时空观被郑重地写入他那本神书《自然哲学的数学原理》中，神书之所以是神书，因为用神书中所描述的定理可以精确地预测月食、日食发生的时间，精确到分秒不差，还能通过计算预言当时尚未被观测到的太阳系行星的存在（海王星），当预言被证实的时候，牛顿本人和他那本神书的声誉达到了空前的顶峰，再没有人怀疑神书中描述的任何事情，牛顿的经典世界观大有千秋万载、一统江湖之势。
然而，就在牛顿死后又过了100多年，一系列的物理实验都得到了让人匪夷所思的结果，这些结果如此地让物理学家诧异以至于一次次地怀疑自己的实验设备是不是出了问题，但是所有的实验被一再地重复，而且实验结果都在无情地推翻着牛顿的绝对时空观，整个物理界都开始陷入了疯狂，物理学遇到了前所未有的危机。如若牛顿地下有知，一定会说：“上帝啊，这一切到底是怎么了？”
如果说到目前为止，本书所说的一切都还让你觉得这个世界就是我所认识的那个天经地义的世界，那么，接下来发生的一切，都将慢慢颠覆你的常识，挑战你的思维底线。